I first learned about the Rule of Four, or “GNAW” approach to analyzing functions from Dr. Doug Brumbaugh, at the University of Central Florida (1993). Students are asked to use multiple representations in modeling mathematics at every level. Since this skill has become increasingly important through the changes to mathematical practices and standards, I like to teach students to G.N.A.W. on their function analysis problems. The “Rule of Four” strategy will help your students make connections and gain a deeper conceptual understanding related to modeling mathematics and solving problems. I love the interaction that occurs among teachers and students, and between students, each and every time I have used this method/strategy. You’ve got to try it!
What is GNAW and the Rule of Four?
The “Rule of Four” or G.N.A.W. Approach was developed at Harvard University (The Harvard Consortium) as a teaching strategy. This method requires students to show their thinking about functions through four different representations. Students learn to represent mathematics in graphic, numeric, algebraic, and verbal (words) formats, gaining the mnemonic “G.N.A.W.” If you want to research the development of this strategy which began around 1986, you can read Calculus, A Pump, Not a Filter, Calculus for a New Century, or the evaluation notes from the Technology Intensive Calculus for Advanced Placement (TICAP)
Why should you use the GNAW approach?
By implementing this process, your students will gain a deeper understanding of mathematics. They will begin to see the connections between each representation, because they learn to practice this skill with purposeful intent. The Rule of Four also helps your students validate the concepts and techniques being taught. Every math teacher in your school (department) can use the GNAW activities to reinforce and build mathematical thought. Even Pre-Algebra and Algebra 1 students, or younger, can find success with this method.
Teachers model this approach during instructional time to set the “tone” for expected thinking and reasoning. Below you can see how an early Algebra GNAW for Quadratic Functions can be differentiated and spiraled up to an Algebra 2 Rational Functions unit. When your math department buys into the benefits, your students’ mathematical thought processes improve schoolwide.
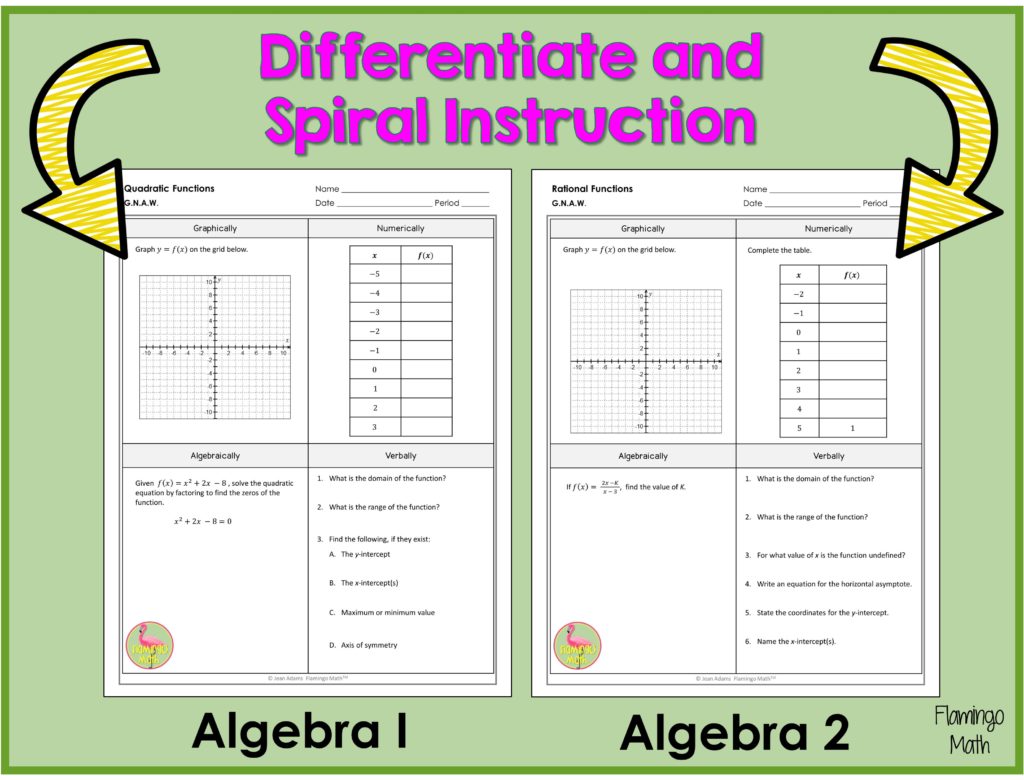
How can you use the Rule of Four?
I like to use a sheet of paper with four blocks. One block or section for each representation: graph, table or mapping (numeric), algebra, verbal (words). Then, you simply give them information in one of the four sections and build your questions based on the course you teach. Remember, it’s important to give your students many, many chances to practice the techniques. By offering multiple opportunities to use this strategy, your students will learn to make connections between the different representations. Here’s a few examples for how I used this method to develop student thinking in my PreCalculus and AP Calculus classes. Notice how the function is the same, just the rigor and questioning has been increased for the Calculus students.
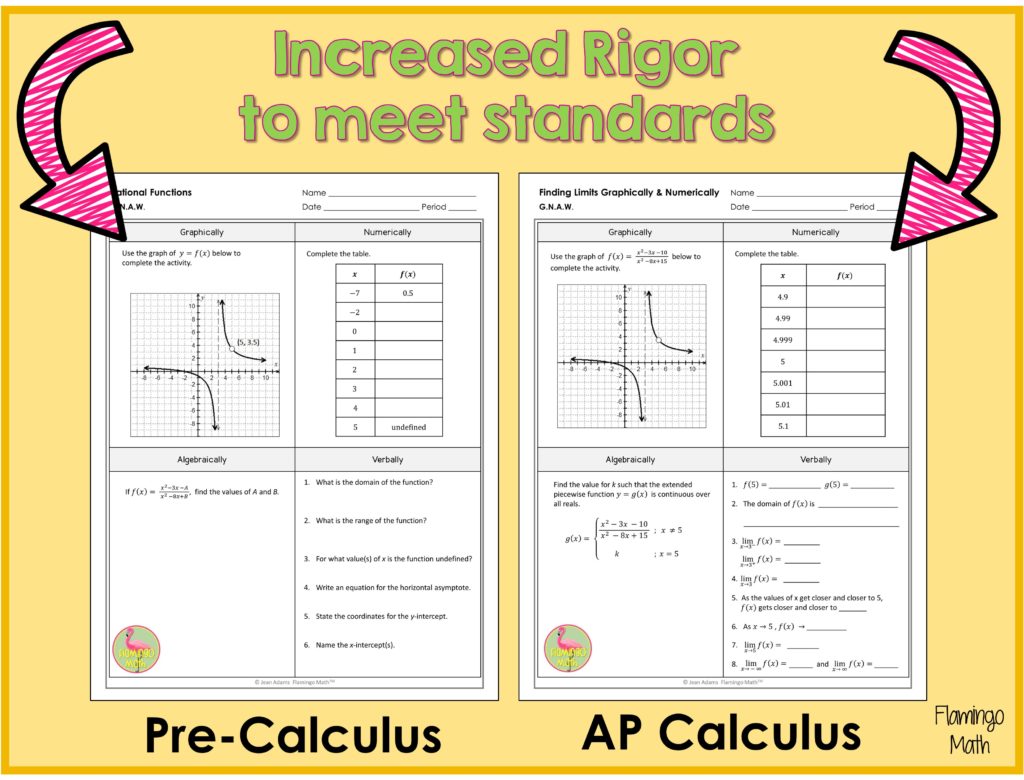
What next?
You too, can create a year-long attitude of exploring concepts using the G.N.A.W. method. Remember, simply give students a place to begin and add a set of instructions for each of the other two or three representations. You can use options of a Rule of Three or a Rule of Four, depending on the student ability level, the difficulty of the task, and the time you have to spend in your class.
For example, say you want students to understand and investigate parabolic behavior.
Graphically: Let’s say you begin with the quadratic function y = x2– x -12
Numerically: Give a set of x-values to find y-values that include both x-intercepts and y-intercepts. Students will use the function to complete the table.
Algebraically: Ask students to factor and solve the function. They will notice the connection in the table between the intercepts from the table of values.
Verbally: Have students describe key features of the function such as domain, range, vertex, intercepts. This is a great place to ask them to explain or justify their thought processes.
If you are interested in giving the Rule of Four/GNAW Activities a try, you can find some of these in my Flamingo Math Store. You can also get the examples shown in this post free by signing up for my FREE RESOURCE LIBRARY.
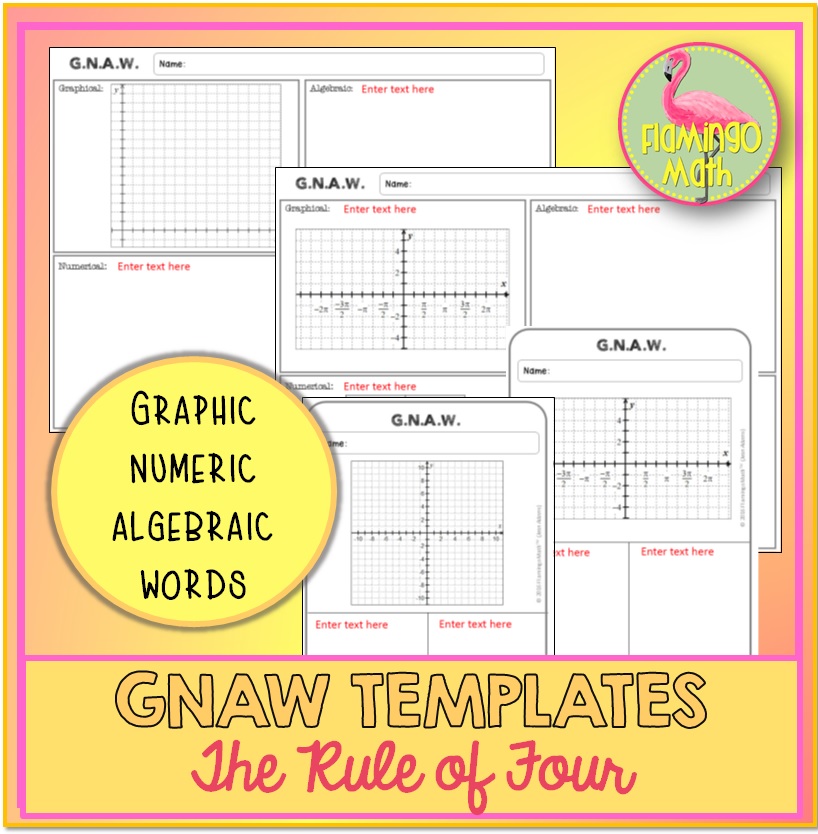
If you want to create your own unique activities, check out these GNAW and the Rule of Four Editable Templates. There are both landscape and portrait styles, trigonometric graphs, and so much more.
Don’t forget to sign up for the newsletter. You will find many other free GNAW and Rule of Four exercises there. Here are four more you can preview for your students. Systems of Equations and Quadratic Functions for Algebra 1 or Algebra 2, Limits and Continuity and Rates of Change for PreCalculus and Calculus students.



Let me know how this works in your classroom.




