Riding the Waves: A Guide to Conquering Slope Fields in AP Calculus

Slope fields, sometimes known as direction fields, are a powerful visual tool in AP Calculus. They can sometimes feel like an impossible puzzle to our students. Fear not! With a keen eye for clues and a systematic approach, you can master these graphical representations of differential equations. Let’s look at some tools that will equip students with the strategies and calculator tips they need to confidently tackle slope field questions on the AP Exam FRQ’s.

What is a Slope Field, Anyway?

Imagine you have a differential equation, say dy/dx=x.  This equation tells you the slope of the tangent line to the solution curve at any given point (x, y). A slope field takes this general idea and visually represents it on a grid. At various points in the xy-plane, you draw a short, uniform-length line segment whose slope is determined by the differential equation at that specific point.

When you connect these tiny line segments, they form a “field of slopes”that show the general direction of the
solution curves.

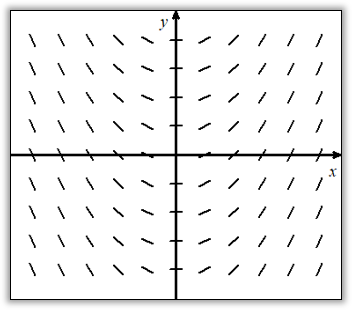
A Family of Curves

If we think of this field like a river: The slope field
shows you the direction of the current at every point, and the solution curves are the paths an object would take as it floats downstream.

Can you see the family of curves that are related to the slope field for  $\frac{dy}{dx}=x$ shown, at right?
The family of curves that satisfy the differential
equation is $F(x)=x^2 +C$.

Step-by-Step Mastery for the AP Calculus Exam:

When you see a slope field on the AP Exam, it’s usually a Multiple Choice “matching game” or a Free Response “Sketch the Solution” task.

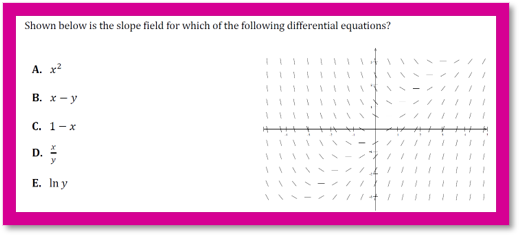
Use these three “tests” in order:

Test A: The “Zero Slope” Hunt (The Horizontal Test)

Look at the graph. Where are the segments perfectly horizontal?

•If they are horizontal all along the y-axis, the equation must involve x in a way that equals zero when $x=0$
(e.g. $\frac{dy}{dx}=x$ or $x^2$).

•If they are horizontal all along the line $y=x$, then the equation is likely something like $\frac{dy}{dx}=y-x$ .

Test B: The “Quadrant” Sign Test

Pick a point in Quadrant IV $(+x,-y)$

• Look at the slope segment: Is it pointing up (positive) or down (negative)?

• Plug a positive x and a negative y into your answer choices.  If the result gives you a negative number but the graph shows a positive slope, cross that choice off immediately!

Test C: The “Isocline” Patterns

• Vertical Consistency: If all the slopes in a vertical column are the same, the equation only depends on x. (e.g.,  $\frac{dy}{dx}=x^2$
• Horizontal Consistency: If all the slopes in a horizontal row are the same, the equation only depends on y (e.g., $\frac{dy}{dx}=y+1$ ).

Practice Strategy: The “Reverse Engineer”

To truly master this for the AP Exam, try this exercise using the Desmos Slope Field Generator:

1. Type $g(x,y)=sin(x)$. Observe how the slopes only change as you move left-to-right.

2. Change it to $g(x,y)=sin(y)$. Observe how they now only change as you move up-and-down.

3. Change it to $g(x,y)=x+y$. Notice the “zero slope” diagonal line where y=-x.

Sketching a solution curve on a slope field is essentially playing a game of “Connect the Dots,” but with one major rule: the field is the boss. You aren’t just drawing a line; you are following a flow.

Grab This Free Matching Worksheet!

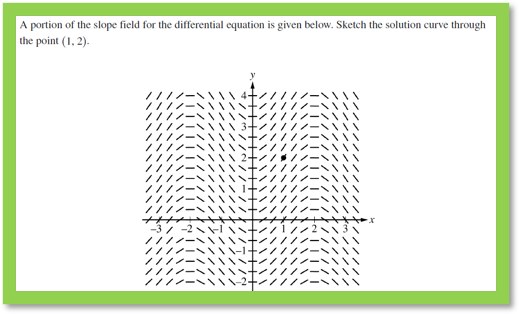
FRQ Strategy: Sketching a Solution Curve

On the AP Exam, you are typically asked to sketch a solution curve passing through a specific initial condition, such as (0, 1). Here is the refined, step-by-step process to ensure you get full credit on an FRQ.

This is often the second part of a slope field FRQ.

1. Locate the Initial Condition: The problem will give you an initial condition, (e.g., $y(0)=1$ ). Find the point $(0, 1)$ on the slope field.
2. “Follow the Arrows”: Starting from the initial condition, draw a curve that is tangent to the small line segments as you move along. Imagine you’re a leaf floating in a stream, and you’re just following the current.
3. Extend in Both Directions: Try to extend the curve as far as the field allows, both to the right and to the left of the initial point.
4. Smoothness and Tangency: Ensure your curve is smooth and that its tangent at any point matches the direction of the slope segment at that point. Avoid jagged lines or abruptly changing directions.

Pro-Tips for the AP Exam

• Don’t “Connect” Every Dash: You aren’t drawing a staircase. Your curve should be a single, smooth, continuous line. Think of the slope segments as “wind” blowing your pen in a certain direction.
• Stay in Bounds: Usually, the FRQ will ask you to sketch the curve within the domain provided by the grid. Don’t stop halfway! Extend it until you hit the edge of the graph or a vertical asymptote.
• Watch for dy/dx=undefined: If you see a column of vertical dashes or empty spaces where the denominator of your differential equation is zero, your curve might have a vertical tangent or a “do not cross” zone.

You will also get this

FREE HOT TOPICS

Graphic Organizer

Let us know your thoughts and ideas for teaching slope fields to students!